tags: ultraproducts

Intriguing use of ultraproducts:

• Denef-Lipschitz proof of Artin approximation: one, two (follow ups by Schoutens);
• Robinson’s proof of Siegel theorem;
• Mustata’s limits of log-canonical thresholds;
• Arapura’s paper on Frobenius amplitudes ;
• Deligne’s categories \(S_t\);
• Kanel-Belov’s work on Dixmier conjecture;
• Olivier Fabert’s non-standard dimensional functional spaces and Gromov squeezing.

Somewhat understandable use of ultraproducts:

• sofic groups via metric ultraproducts;
• van den Dries-Wilkie’s construction of asymptotic cones;
• Goldbring’s local Hilbert 5th problem and Hrushovski’s Lie models.

(comments)

tags: Abelian varieties, positivity

I’ll throw in some coordinate-free-ness, for originality’s sake, and because I hate matrices.

Let \(V\) be a complex vector space and let \(\Lambda\) be a finitely generated torsion-free Abelian group such that \(\Lambda \otimes \mathbb{R}\cong V\) as \(\mathbb{R}\)-vector spaces. The data of \(V\), \(\Lambda\) and a Hermitian form \(H: V \otimes V \to \mathbb{C}\) such that \(H|_{\Lambda \times \Lambda} \subset \mathbb{Z}\) gives rise to an Abelian variety and a line bundle endowed with a Hermitian metric.

The inclusion \(\Lambda \hookrightarrow V\) extended linearly to a map of \(\mathbb{R}\)-spaces \(\Lambda \otimes \mathbb{R}\to V\) is denoted \(\Pi\).

Let \(A \in GL(\Lambda)\) be an intergral linear invertible self-map such that \((Ax, y) = -(x,Ay)\) wrt the standard inner product on \(\Lambda\). Via \(\mathbb{R}\)-linear extension this induces a symplectic form on \(V\), call it \(\omega\). Define the following Hermitian metric on \(V\) \[ H(x,y) = \omega(Ix,y) + i \omega(x,y) \] where \(I\) is the complex structure on \(V\). One checks that it is \(\mathbb{C}\)-linear in the first argument, \(\mathbb{C}\)-antilinear in the second. Further, \[ H(x,y) = \overline{H(y,x)} \qquad \textrm{ iff }\qquad \omega(Ix,Iy) = \omega(x,y) \]

Indeed, \[ H(y,x) = \omega(Iy,x) + i \omega(y,x) = -\omega(x,Iy) - i \omega(x,y) \] and \(-\omega(x,Iy) = \omega(Ix,y)\) iff \(\omega(Ix,Iy) = \omega(x,y)\).

Since \(\Pi\) is an isomorphism and in particular surjective, in order to check that \(H\) is Hermitian we need to check that \(\omega(I \Pi x, I \Pi y) = \omega(\Pi x, \Pi y)\) for all \(x,y \in \Lambda \otimes \mathbb{R}\). Remark now that from definition of \(\omega\), \(\omega(\Pi x, \Pi y)=(Ax,y)\).

Pass to the complexification: let \(\Pi \otimes \mathbb{C}: (\Lambda \otimes \mathbb{R}) \otimes_{\mathbb{R}} C \to V \otimes_{\mathbb{R}} \mathbb{C}\) be the \(\mathbb{C}\)-linear extension of \(\Pi\). The vector space \(V\) decomposes into direct sum of eigenspaces of \(I\): \(V = V^{1,0} \oplus V^{0,1}\) where \(I\) acts by \(i\) on the first piece and by \(-i\) on the second. Denote \(\Pi' := \pi_{V^{1,0}} \circ \Pi \otimes \mathbb{C}\). By definition, \(\Pi'\) is the same as the composition of \(\Pi\) and identification between \(V \subset V \otimes C\) and \(V^{1,0}\) via the projection on \(V^{1,0}\). When written out in some basis \(\Pi'\) is called a period matrix. If \(\Lambda \cong \mathbb{Z}^{2g}\), it is a \(g \times 2g\) matrix which has the coordinates of the generators of \(\mathbb{Z}^{2g}\) as its columns.

\[ \begin{array}{ccccc} \Lambda \otimes \mathbb{R}& \to^\Pi & V & \to & V \otimes \mathbb{C}\\ \downarrow & & \downarrow & \swarrow & \\ \Lambda \otimes \mathbb{C}& \to^{\Pi'} & V^{1,0} & \\ \end{array} \]

After restriction to \(V^{1,0}\) it is clear that \(\omega\) respects \(I\) if and only if \(\omega_\mathbb{C}(i \Pi' x, i \Pi'y) = \omega_\mathbb{C}(\Pi' x, \Pi'y)\) for all \(x,y \in \Lambda \otimes C\).

Define \[ J = (\Pi\otimes \mathbb{C})^{-1} (I\otimes \mathbb{C}) (\Pi\otimes \mathbb{C}) \] Notice that it has the property \(i \Pi' = \Pi' J\). Also notice that \(\omega_\mathbb{C}(\Pi' x, \Pi' y) = (Ax, y)\). Then the condition to check becomes \[ (A J x, J y) = (A x, y) \] or \(J^* A J=A\). Rewrite the latter identity using the definition of \(J\), denoting \(\Phi = \Pi \otimes \mathbb{C}\) \[ \Phi^* (I\otimes \mathbb{C})^* (\Phi^{-1})^* (A \otimes \mathbb{C}) \Phi^{-1} (I\otimes \mathbb{C}) \Phi = A \] so, using self-adjointness of \(I \otimes \mathbb{C}\), \[ I\otimes \mathbb{C}(\Phi^{-1})^* (A \otimes \mathbb{C}) \Phi^{-1} (I\otimes \mathbb{C}) = (\Phi^{-1})^* A \Phi^{-1} \] and further (omitting \(\otimes \mathbb{C}\) for simplicity of notation) \[ I (\Phi A^{-1} \Phi^*)^{-1} I = (\Phi A^{-1} \Phi^*)^{-1} \] Given that \(I \otimes \mathbb{C}\) is semi-simple, the restriction of \((\Phi A^{-1} \Phi^*)^{-1}\) to \(V^{1,0}\) must take values in \(V^{0,1}\) (if the projection of \((\Phi A^{-1} \Phi^*)^{-1}(x)\) on \(V^{1,0}\) is non-zero element \(y\), then \(i y i = y\) which is absurd), and similar reasoning works for \(V^{0,1}\). We conclude, computing \(\pi_{1,0} \circ (\Phi A^{-1} \Phi^*)^{-1}\) and \(\pi_{0,1} \circ (\Phi A^{-1} \Phi^*)^{-1}\), that \[ \Pi' A^{-1} (\Pi')^* = 0 \textrm{ and } \overline{\Pi'} A^{-1} (\overline{\Pi'})^* \] [the trick is to write down the operator to be inverted as an inverse of block matrix, and observe that the “determinant” term does not matter for vanishing] The second equality is the conjugation of the first, and we are done clarifing the condition for \(H\) to be Hermitian.

Now let us compute \(H(x,x)\). As before it will be convenient to pass to the complexification of \(\omega\) and put \[ H_\mathbb{C}(x,y) = \omega_\mathbb{C}(I \otimes \mathbb{C}x, y) +i \omega_\mathbb{C}(x,y) \] The second term is defined by the proprety: \(\omega_\mathbb{C}(\Phi x, \Phi y) = (Ax,y)\), and hence \[ \omega_\mathbb{C}(x, y) = (A\Phi^{-1}x,\Phi^{-1}y) \] so \[ \omega_\mathbb{C}(x, y) = ((\Phi^{-1})^* A \Phi^{-1}x, y) = ((\Phi A \Phi^*)^{-1} x, y) \] And so the first term is: \[ \omega_\mathbb{C}(I \otimes \mathbb{C}x, y) = ((\Phi^* A \Phi)^{-1} (I \otimes \mathbb{C})x, y) \] Assuming \(H\) to be Hermitian, the restriction of \((\Phi^* A^{-1} \Phi)^{-1}\) to \(V^{1,0}\) writes \((\Pi' A^{-1} (\overline{\Pi'})^*)^{-1} ) D\), and its restriction to \(V^{0,1}\) is \((\overline{\Pi'} A^{-1} (\Pi')^*)^{-1}\). Therefore \(H(x,x)\) is \[ (2i (\Pi' A^{-1} (\overline{\Pi'})^*)^{-1} x,x) \] on \(V^{1,0}\). Since positivity depends only on the sign of eigenvalues, passing to the inverse operator does not affect it, and so the condition for positivity of \(H\) is \[ (i (\Pi' A^{-1} (\overline{\Pi'})^*)^{-1} x,x) > 0 \] for all \(x \in V \hookrightarrow V \otimes \mathbb{C}\).

(comments)

tags: non-Archimedean geometry

Let \(K\) be an algebraically closed complete non-Archimedean valued field. Let \(q \in \mathbb{G}_m(K)\) be an element of strictly positive valuation. Then the quotient \(\mathbb{G}_m(K) / q^{\mathbb Z}\) is a rigid analytic manifold which can be embedded into \(\mathbb{P}^2(K)\) by means of analytic functions \(x, y: \mathbb{G}_m(K) \to \mathbb{A}^2(K)\) that are periodic under multiplication by \(q\) (one takes the image in \(\mathbb{A}^2\) and takes the closure in \(\mathbb{P}^2\)). Here is the series that give \(x\) (taken from Tate’s article ``A review of non-Archimedean elliptic functions’’): \[ x(w) = \sum_{q = -\infty}^{\infty} \dfrac{q^m w}{(1 - q^m w)^2} - 2 \sum_{m=1}^\infty \dfrac{q^m}{(1 - q^m)^2} \]

Recall that algebras of the form \[ K\{x_1, \ldots, x_n\} := \{\ \sum a_\delta x^\delta \ \mid\ v(a_\delta) \to \infty \textrm{ as } |\delta| \to \infty\ \} \] where \(\delta\) is a multiindex, are called Tate algebras. They are normed algebras with the norm \[ || \sum a_\delta x^\delta || = \sum e^{-v(a_\delta)} \]

The power series that constitute these algebras converge on unit polydiscs \[ \{\ x_i \in K \ \mid\ ||x_i|| \leq 1 \ \} = \{\ x_i \in K \ \mid\ v(x_i) \geq 0 \ \} \] Variants include (isomorphic) algebras \[ K\{e^{-r_1}x_1, \ldots, e^{-r_n}x_n\} := \{\ \sum a_\delta x^\delta \ \mid\ v(a_\delta) \to \infty \textrm{ as } |\delta| \to \infty\ \} \] of functions analytic on polydiscs of varying radii \[ \{\ x_i \in K \ \mid\ v(x_i) \geq r_i\ \} \] They are however not isometric, since they are normed in a different way \[ || \sum a_\delta x^\delta || = \sum e^{-v(a_\delta)} e^{-r_{\delta_i}} \]

An annulus with inner valuative radius \(a\) and outer valuatie radius \(0\) \[ \{\ x \in K \ \mid\ 0 \leq v(x) \leq a\ \} \] is an affinoid domain with the corresponding algebra of analytic functions \(K\{x, y\}/(xy = \gamma)\); here, \(\gamma \in K\) is such that \(v(\gamma) = a\).

This is an example of a rational domain in \(\mathbb{A}^1\). The importance of rational domains lies in the following theorem:

Theorem (Gerritzen-Grauert). Let \(U\) be an affinoid domain. Every affinoid subdomain of \(U\) is a finite union of rational subdomains of \(U\).

An affinoid algebra is a quotient of a Tate algebra by a closed ideal. Global analytic functions on affinoid domains are called affinoid functions. Recall that a function is called meromorphic on a domain if it can be locally represented as a quotient of analytic functions. We will see that on affinoid domains meromorphic functions are quotients of affinoid functions globally.

Intersections of affinoid domains are affinoid. Affinoids play the role of opens in rigid geometry. In fact, one can define the ``rigid \(G\)-topology’’: it is a Grothendieck topology where admissible covers are finite covers of \(\mathrm{Specm} A\) by affinoid domains.

Both elliptic functions introduced above, \(x\) and \(y\), are meromorphic on \(\mathbb{G}_m(K)\). Indeed, restricting to annuli \[ \{\ x \in K \ \mid\ n \leq v(x) \leq m\ \} \] for \(n,m \in \mathbb{Z}\), functions \(x\) and \(y\) have finitely many poles, therefore, after multiplication by a suitable polynomial, they become analytic.

Note that \(x\) and \(y\) cannot be extended to a function meromorphic on \(\mathbb{A}^1\) (or unit disc), since their poles converge to 0, and meromorphic functions can only have isolated poles (the proof is similar to the Archimedean case).

Quite expectedly though, they can be uniquely extended to the punctured unit disc. It took me some effort to find out how this can be proved: analytic continuation works quite differently in non-Archimedean situation than in the complex-analytic setting.

Theorem (Tate acyclicity theorem) Let \(\{ A_i \}\) be finitely many affinoid domains such that \(\cup A_i = A\). Then the following sequence (with Čech differentials: taking restrictions with alternating signs) is exact \[ 0 \to \mathcal{O}_A(A) \to \mathcal{O}_A ( \coprod A_i) \to \mathcal{O}_A ( \coprod A_i \cap A_j) \] where \(\mathcal{O}_A\) is the sheaf of affinoid functions. In particular, affinoid domains are acyclic and cohomology of coherent sheaves in \(G\)-topology can be computed using Čech complex of an admissible covering.

Theorem (Kiehl’s Theorem A) Any coherent sheaf \(\mathcal F\) over an affinoid domain is generated by global sections.

Proof. Let \(a \in A\) and let \(\mathcal{I}_{a}\) be the skyscraper sheaf. Consider the exact sequence \[ 0 \to \mathcal{I}_a \mathcal F \to \mathcal F \to \mathcal F / \mathcal{I}_a \mathcal F \to 0 \] Then the associated cohomology long exact sequence is \[ \ldots \to H^0(A,\mathcal F) \to H^0(A,\mathcal F / \mathcal{I}_a \mathcal F) \to H^1(A,\mathcal{I}_a \mathcal F) \to \ldots \] where the last term vanishes by Tate’s acyclicity. Therefore, there exist (finitely many, by coherence) non-vanishing at \(a\) global sections of \(\mathcal F\). The second term is a finitely generated \(\mathcal{O}_{A,a}\)-module, and by Nakayama’s lemma, these sections generate the germs of \(\mathcal F\) at \(a\).

Read more (comments)

tags: model theory, curves

Abstract projective geometry

Let \(k\) be a field. Consider the set of points \(P\) and lines \(L\) on the projective \(n\)-space \(\operatorname{\mathbb{P}}^n(k)\) over \(k\). One finds that the following properties hold:

• there is exactly one line incident to any two distinct points
• there is exactly one point that is incident to two distinct lines
• every line contains at least three distinct points

A tuple \((P,L,I)\) where \(P\) is the set of points, \(L\) is the set of lines and \(I \subset P \times L\) is the incidence relation, is an abstract projective geometry if the properties above hold. These properties in particular hold if \(P\), \(L\) are sets of points and lines on a projective plane over a (skew) field \(k\). There are examples of abstract projective geometries that do not arise this way. The reason is that all geometries arising from a (skew) field additionally satisfy Desargues axiom:

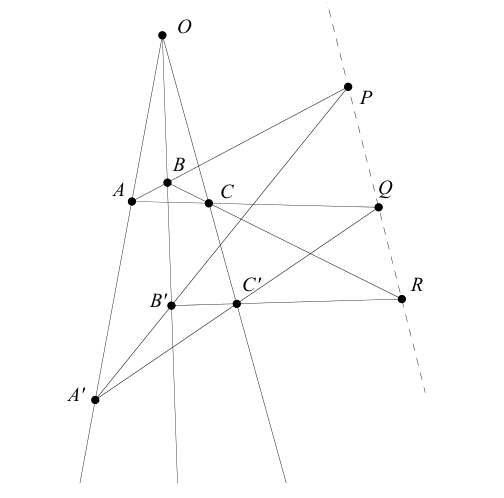
Given two triangles \(ABC\) and \(A'B'C'\) as above, the lines \(AB\) and \(A'B'\), \(BC\) and \(B'C'\), and \(AC\) and \(A'C'\) intersect in three points that lie on the same line.

There are two affine statements that follow from this axioms: called small and big Desargues axioms.

small Desargues: given \(A\) and \(A'\), \(B\) and \(B'\), \(C\) and \(C'\) lying on three parallel lines, \(BC\) and \(B'C'\) are parallel.

big Desargues: given that the lines \(AB\) and \(A'B'\), and \(AC\) and \(A'C'\) are pairwise parallel, the lines \(BC\) and \(B'C'\) are parallel.

If \(k\) is commutative, then a Pappus axiom is also satisfied:

Read more (comments)

Site generated by Hakyll