Incidence structures on algebraic curves

Posted on June 7, 2016 by Dima

Abstract projective geometry

Let \(k\) be a field. Consider the set of points \(P\) and lines \(L\) on the projective \(n\)-space \(\operatorname{\mathbb{P}}^n(k)\) over \(k\). One finds that the following properties hold:

there is exactly one line incident to any two distinct points
there is exactly one point that is incident to two distinct lines
every line contains at least three distinct points

A tuple \((P,L,I)\) where \(P\) is the set of points, \(L\) is the set of lines and \(I \subset P \times L\) is the incidence relation, is an abstract projective geometry if the properties above hold. These properties in particular hold if \(P\), \(L\) are sets of points and lines on a projective plane over a (skew) field \(k\). There are examples of abstract projective geometries that do not arise this way. The reason is that all geometries arising from a (skew) field additionally satisfy Desargues axiom:

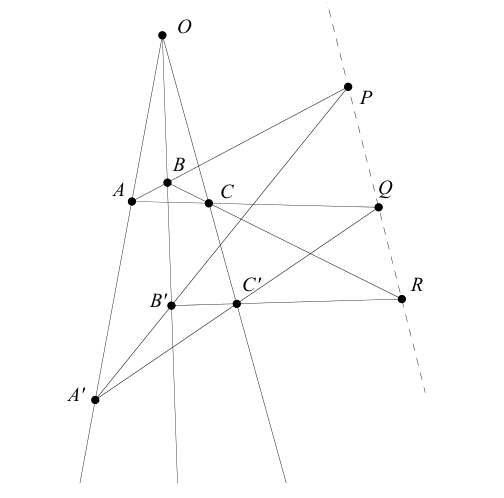
Given two triangles \(ABC\) and \(A'B'C'\) as above, the lines \(AB\) and \(A'B'\), \(BC\) and \(B'C'\), and \(AC\) and \(A'C'\) intersect in three points that lie on the same line.

There are two affine statements that follow from this axioms: called small and big Desargues axioms.

small Desargues: given \(A\) and \(A'\), \(B\) and \(B'\), \(C\) and \(C'\) lying on three parallel lines, \(BC\) and \(B'C'\) are parallel.

big Desargues: given that the lines \(AB\) and \(A'B'\), and \(AC\) and \(A'C'\) are pairwise parallel, the lines \(BC\) and \(B'C'\) are parallel.

If \(k\) is commutative, then a Pappus axiom is also satisfied:

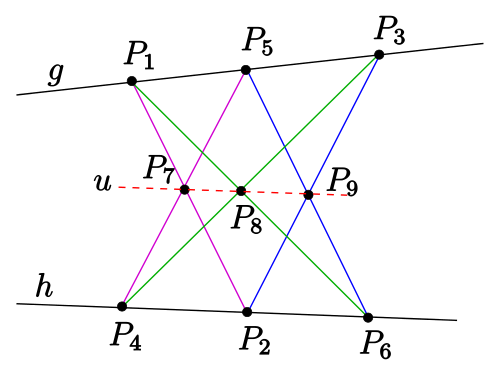
The axiom states that in the configuration as above the three points \(P_7, P_8\) and \(P_9\) lie on the same line.

Theorem. If \(\mathfrak{G} = (P, L, I)\) is an abstract projective geometry which satisfies Desargues axiom then there exists a skew field \(k\) such that \(P = \operatorname{\mathbb{P}}^n(k)\), \(n > 1\). If \(\mathfrak{G}\) also satisfies the Pappus axiom, then \(k\) is commutative, i.e. is a field.

The proof of this theorem is nicely exposed in Hartshorne’s notes called “Foundations of projective geometry” and in the classical Emile Artin’s book “Geometric algebra”.

I will now sketch the main steps of the proof.

Let \(A = (P,L, I)\) be an affine geometry. A dilation is an automorphism of \(A\) such that every line is parallel to its image. In projective terms, the infinite line is fixed. A homothety is a dilation with one affine fixed point.

On an affine plane over a field \(k\) the set of dilations forms the group \(\operatorname{\mathbb{G}}_m(k) \rtimes \operatorname{\mathbb{G}}_a(k)\).

Theorem: a dilation is determined by its action on two points.

A translation is a dilation with no (affine) fixed points. Translations form a normal subgroup of the group of dilations of an affine plane. For an affine plane over a field this subgroup is \(\operatorname{\mathbb{G}}_a(k)\).

If small Desargues axiom holds then for any two points \(P, P'\) there exists a unique translation that maps \(P\) to \(P'\). It follows that translations form an Abelian group.

Assuming big Desargues axiom, and given three points \(O, P, P'\) such that \(P, P' \neq O\), there exists a unique dilation that fixes \(O\) and maps \(P\) to \(P'\).

The additive group of the field is reconstructed as the group of translations, with the group of homotethies (isomorphic to the multiplicative group) acting on it. More concretely, fix a line \(l\), and fix two points, call them \(0\) and \(1\). The set of points of \(l\) will be our field. In order to add two points \(x\) and \(y\), take two translations \(\tau_x, \tau_y\) that send 0 to \(x\) and \(y\) respectively, and put \(x+y\) to be the result of the application of \(\tau_x \circ \tau_y\) to \(0\). To multiply, let \(\mu_x, \mu_y\) be homotheties that fix \(0\) and send \(1\) to \(x\) and \(y\). Then \(x \cdot y\) is defined as \(\mu_x \circ \mu_y (1)\).

Desargues axiom is used to show the distributivity, and Pappus axiom is used in order to show commutativity of the group of dilations.

Recently, the Main theorem of Abstract Projective Geometry has been used by Bogomolov and Tschinkel in one of the key steps of the proof of the function field reconstruction theorem. The birational anabelian program seeks to reconstruct function fields of varieties of dimension \(> 2\) over the algebraic closure of \(\mathbb{F}_p\) from their absolute Galois groups. If \(K\) is the function field of such variety then one notices that \(K^\times / k^\times\) is an infinite-dimensional projective space with an Abelian group structure. The absolute Galois group of \(K\) induces enough structure on the projective space \(K^\times/k^\times\) so that an isomorphism on absolute Galois groups induces a map that preserves the incidence relation. The main theorem of Abstract Projective Gemotry then allows to conclude that the map is induced by a field isomorphism (up to inseparable extensions).

Zariski geometries

What if we want to look at the incidence systems of curves of higher degree? A generalisation of main theorem of Abstract Projective geometry is possible if we agree to work over an algebraically closed field.

One uses the language of mathematical logic. Let \(M\) be a first-order structure such that a Noetherian (proper descending chains of closed irreducible sets must be finite) topology is defined on every Cartesian power \(M^n\). Assume that every closed set is named by a predicate, so that every constructible set is definable. Further assume that every definable set is constructible.

An example of such structure is the so-called full Zariski structure on an algebraic variety \(V\) over an algebraically closed field \(k\): name every Zariski closed subset of \(V^k\), \(k \geq 1\) by a predicate.

Question: given a full Zariski structure on an algebraic variety \(V\), is it possible to recover the field \(k\)?

Here is more precise definition of “recover” which is a standard notion in model theory. A first-order structure \(M\) interprets a field, if there exists a definable subset \(F \subset M^n\) and a definable equivalence relation \(R \subset F \times F\) such that \(R/F\) can be endowed with definable addition and multiplication maps which make it into a field.

Theorem (Hrushovski, Zilber). Let \(M\) be an irreducible algebraic curve over an algebraically closed field \(k\), considered as a full Zariski structure. Then \(M\) interprets a field, definably isomorphic to \(k\).

This is actually a corollary of a more general theorem of Hrushovski and Zilber, which describes axiomatically a class of structures, similar to full Zariski structures which interpret a field.