tags: physics

Being confused for a long time about the main aspects of quantum mechanics and quantisation, I decided now to summarise my current knowledge.

So, dear diary, non-relativistic classical mechanics essentially equals symplectic geometry. To be totally honest, while a symplectic manifold captures all the relevant information about a mechanical system, it only appears as result of a complete understanding of the system. If one wishes to derive the equations of motion from fundamental principles then one proceeds as follows.

Take a manifold (probably a Riemannian manifold) which describes possible positions of elements of your mechanical system. Trajectories are just curves in this manifold. Knowing that your system is in a state \(x_0\) we need to understand how it will evolve in time. So we have a functional called action on the space of possible trajectories obtained by integrating something called Lagrangian density over the curve. The principle of least action says that the system will evolve according to the path which minimizes the action; the differential equations of motion are called the Euler-Lagrange equations. One can prove a theorem that for mechanical systems of a certain kind (? not sure what are the precise requirements here) the trajectories can be described in a particularly nice way as curves parallel with respect to Hamiltonian flow on a symplectic manifold. The translation from Riemannian to symplectic picture is called Legendre transform.

Read more (comments)

tags: moduli, formal schemes

One is often interested whether a covariant functor \(F\) from the category of (affine) schemes to the category of sets can be represented by a scheme so that \(F(X) = h_S(X) = \mathrm{Hom}(X, S)\). It is natural to assume that all sensible functors are locally of finite presentation, that is, preserve inverse limits.

Passing to the opposite category of rings, it means that the contravariant functor \(F^{\mathrm op}\) from rings to sets turns direct limits into inverse limits. This is going to be useful for the following reason: any ring is a direct limit of its finitely generated (over some base) subrings, and so, any object \(\xi \in F^{\mathrm op}(R)\) will be defined over a finitely generated subring \(\xi \in F^{\mathrm op}(R_i)\), for \(F^{\mathrm op}(\varinjlim R_i) \cong \varprojlim F^{\mathrm op}(R_i)\). Example: let \(\mathcal{A}\) be the functor on the category of \(k\)-algebras such that \(\mathcal{A}(R)\) be the set of isomorphism classes of polirized Abelian varieties over \(X=\mathrm{Spec}\,R\). Then a particular \(\xi \in \mathcal{A}^{\mathrm op}(R)\) is defined by some equations with coefficients that belong to a finitely generated over \(k\) algebra \(R_i\).

Let \(R\) be a local ring with the maximal ideal \(\mathfrak m\). An infinitesimal deformation is an element \(\xi \in F(\mathrm{Spec}\,R/(\mathfrak{m}^n)\) for some \(n > 1\). A formal deformation is a sequence of compatible elements \(\xi_i \in F(\mathrm{Spec}\,R/(\mathfrak{m}^n))\). An effective formal deformation is an element \(\xi \in F(\mathrm{Spec}\,\hat R)\), where \(\hat R = \varprojlim R/(\mathfrak{m}^n)\) so in particular an effective formal deformation is a deformation.

Read more (comments)

tags: non-Archimedean geometry

Let \(k\) be a field. Recall that a valuation \(v: k \to \Gamma\), for \(\Gamma\) an ordered Abelian group, is a group homomorphism \(v: k^\times \to \Gamma\) such that \[ v(x + y) \geq \min\{v(x), v(y) \} \] When \(\Gamma=\mathbb{Z}^n\) then the valuation is called rank \(n\) valuation. In classical terminology rank 1 valuations are just ``valuations’’. If the homomorphism is partial, then \(v\) is called a semi-valuation.

Let \(X\) be an algebraic variety over a field \(k\). For a fixed valuation \(v_0\) on \(k\), the space of valuations on \(k(X)\) that restrict to \(v_0\) is an interesting object to study. If \(v_0\) is trivial (i.e. \(v(f)=0\) for all \(f \in k^\times\)) then the space of all rank 1 valuations is called Riemann-Zariski space. It is topologized as follows: basic opens are sets of valuations \(v\) such that \(v(f_i) \geq 0\) for a some fixed \(f_1, \ldots, f_n\). Incidentally, RZ space is the inverse limit of all schemes over \(k\) with the given function field.

One can also fix the value group \(\Gamma\) and consider spaces of valuations with values in \(\Gamma\), this way one gets Berkovich spaces (\(\Gamma = \mathbb{R}\)). They are topologized in the way similar to Riemann-Zariski spaces: basic opens are sets of valuations that are non-negative on some finite sets of elements of the field. Hrushovski-Loeser spaces (or spaces of stably dominated types) is a way to regard such valuations from a ``semi-algebraic’’ point of view. The setting is much more general here, valuations are with values in \(\Gamma\) arbitrary (which embeds into some very big ordered group, which is fixed).

Read more (comments)

tags: model theory

There are many statements known as a “group configuration theorem”, all of them involve some setting where the notion of independence exists; the statement is roughly the following: given a collection of tuples with certain inter-dependence relations one can construct an (infinitely) definable group, or a group action, such that a diagram of dependences that canonically arises from a group law (or group action) is related in some way to the given configuration.

We will consider the simplest setting and statement. Suppose we work in a finite rank theory. A collection of tuples \(\{s,t,u,x,y,z\}\) is said to form a group configuration, diagrammatically depicted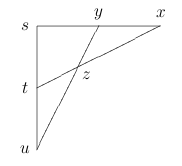

if whenever three tuples are on the same line, their joint dimension is 2, every tuple has rank 1, and all tuples are pairwise independent. This setting is considered in the exposition of Hodges (see the references at the end of the post), and in the article of Evans and Hrushovski.

One should think of elements forming a group configuration as a collection of generic points of 1-dimensional definable sets (or varieties, in the case of the theory of algebraically closed fields). An equivalent piece of data in terms of varieties and correspondences is: \(\alpha_s: X \vdash Y, \beta_t: X \vdash Z, \ast: S \times T \vdash U\) such that \[ \bigcup\limits_{s,t: s \ast t =u} \Gamma(\beta_t \circ \alpha^{-1}_s) \] is one-dimensional (i.e. is a graph of a correspondence \(Y \vdash Z\) for generic \(u \in U\)).

Read more (comments)

Site generated by Hakyll