Hrushovski's group configuration

 Posted on May 14, 2015 by Dima

tags: model theory

There are many statements known as a “group configuration theorem”, all of them involve some setting where the notion of independence exists; the statement is roughly the following: given a collection of tuples with certain inter-dependence relations one can construct an (infinitely) definable group, or a group action, such that a diagram of dependences that canonically arises from a group law (or group action) is related in some way to the given configuration.

We will consider the simplest setting and statement. Suppose we work in a finite rank theory. A collection of tuples \(\{s,t,u,x,y,z\}\) is said to form a group configuration, diagrammatically depicted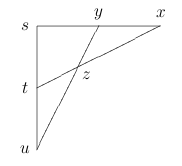
group configuration 1
group configuration 1

if whenever three tuples are on the same line, their joint dimension is 2, every tuple has rank 1, and all tuples are pairwise independent. This setting is considered in the exposition of Hodges (see the references at the end of the post), and in the article of Evans and Hrushovski.

One should think of elements forming a group configuration as a collection of generic points of 1-dimensional definable sets (or varieties, in the case of the theory of algebraically closed fields). An equivalent piece of data in terms of varieties and correspondences is: \(\alpha_s: X \vdash Y, \beta_t: X \vdash Z, \ast: S \times T \vdash U\) such that \[ \bigcup\limits_{s,t: s \ast t =u} \Gamma(\beta_t \circ \alpha^{-1}_s) \] is one-dimensional (i.e. is a graph of a correspondence \(Y \vdash Z\) for generic \(u \in U\)).

If \(\alpha_s\) were graphs of invertible functions (both properties can hold generically), we can define the equivalence relation on \(S \times S\): \[ (s,t) \sim (u,v) \textrm{ iff } \alpha_t \circ \alpha_s^{-1} = \alpha_v \circ \alpha_u^{-1} \] One can then the define a group law on \(S \times S/\sim\): \[ [(s,t)][(u,v)] = [(s',w)][(w,t')] = [(s',t')] \] where \(w\) is some element that does not change the equivalence classes of pairs. In order to prove that such \(w\) exists we require that \(\beta_t\) are generically invertible as well.

So the proof can be broken down in three parts.

Part 1. Suppose \(\alpha, \beta\) are functions \(X \to X\).

The element \(w\) as above would exist for dimension considerations if we could show that \(\dim T \times T/\sim = 1\). In order to do that we have to apply a variant the Stabiliser theorem of Zilber’s.

Stabiliser theorem. Let \(G\) be a definable group of finite rank. Let \(X \subset G\) be a definable subset with only one component of maximal dimension. Consider the set of elements of \(G\) that generically stabilise \(X\) \[ H = \{ g \in G \mid \dim (g X \setminus X) \cup (X \setminus g X) < \dim X\} \] Then \(\dim H \leq \dim X\), and if \(\dim H = \dim X\) then there exists an element \(g\) such that \(\dim (X \setminus g H) \cup (g H \setminus X) < \dim X\).

Proof. By compactness, there exists \(Y\) such that \(H\) is the setwise stabiliser of \(Y\) and \[ \dim (Y \setminus X ) \cup (X \setminus Y) < \dim X \] If \(Y\) intersects a coset of \(H\) properly, then it contradicts the fact that \(Y\) is preserved by \(H\). Then clearly \(Y\) must be a union of cosets of \(H\), and \(Y\) is also irreducible. The conclusion of the theorem follows.

One can rephrase the conditions on the data in a group configuration as follows. We are considering subgroups in the group \(G\) of germs at a generic point of the definable set \(X\). We have two definable subsets of this group \(S,T\) each of dimension 1, we have an equivalence relation \(\sim\) on \(S\times T\) with generically 1-dimensional classes such that \[ \dim \{ st^{-1} \in G \mid (s,t) \sim (s_0, t_0) \} = 0 \] for all \((s_0, t_0) \in G\). First note that the consequence of this is that \(\dim S \cdot T = \{ st \mid s \in S, t \in T\} = 1\).

We now need to show that \(\dim S \times S^{-1} = 1\). By Stabilizer theorem \(\dim T \cap \mathrm{Stab}(S) = 1\), therefore \(S\) is a coset of its stabiliser, and consequently \(\dim S \cdot S^{-1} = \dim S = 1\).

Part 2. Change the configuration to an interalgebraic one such that \(\alpha_s, \beta_t\) are (generically) functions.

Suppose we would like to have in the diagram above that \(z \in \mathrm{dcl} (x,t)\). It seems that aq very natural way to achieve this is to replace \(z\) be canonical basis of \(\mathrm{tp}(z/x,t)\). One way to understand what this canonical base is the following: consider the (definable) set of all Galois conjugates of \(z\) over \(x,t\) and factor it by the action of the symmetric group that permutes the conjugates. The quotient \(z'\) is a tuple that is in the definable closure of \(x,y\) (by Galois invariance). But in order to prove that we obatain a group configuration this way we need to ensure that \(z'\) is interalgebraic with \(z\), i.e. has the same dimension. This can turn out not to be the case if Galois conjugates of \(z\) are independent over the base parameter set.

Here is an example when this happens (in the theory of algebraically closed fields):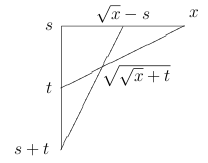

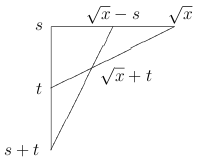
The Galois conjugates \(\sqrt{\sqrt{x}+t}\) and \(\sqrt{-\sqrt{x}+t}\) are independent, and the canonical base of \(\mathrm{tp}(\sqrt{\sqrt{x}+t}/x,t)\) is of rank 2. The solution is to replace \(x\) by \(\sqrt{x}\) in the diagram. Then doing the same trick with the canonical basis we could pass to the diagram

which is a group configuration, and moreover \(\sqrt{x} + t\) is obviously in the in definable closure of \(\sqrt{x}, t\).

Here is how to achieve this in the general situation. The trick is to extend the base parameter set by introducing an element \(s'\) with the same type as \(s\) but independent from it over the rest of the elements of the configuration. Consider then an automorphism \(\sigma\) that maps \(s\) to \(s'\) but fixes \(x,t\), and let \(y'=\sigma(y), u'=\sigma(u)\), so, speaking somewhat imprecisely, \(y'=\alpha_{s'}\) and \(u'=s'\ast t\).

Geometrically that means to introduce copies of \(S\), \(Y\), \(U\) and copies of correspondences \(\alpha, \ast\), \(\alpha_{s'}: X \vdash Y', \ast: S' \times T \to U'\).

Further, replace our group configuration with the configuration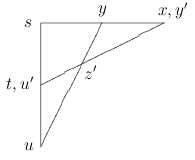

where \(z'\) is the canonical basis of \(\mathrm{tp}(x,t,y',u')\). Clearly, \(y\) and \(y'\), \(u\) and \(u'\) are interalgebraic (over \(s'\)), respectively. Let us check that the dimension of \(z'\) over \(s'\) is 1. Let \(\sigma\) be some element of the Galois group of \(z\) over \(x,t\). Then \(\mathrm{acl}(z, \sigma(z)) \subset \mathrm{acl}(x,t)\) and \(\mathrm{acl}(z,\sigma(z)) \subset \mathrm{acl}(u,y)\), therefore, \(\mathrm{acl}(z) \subset \mathrm{acl}(u',y')\) because automorphisms preserve the dimension. If \(\mathrm{acl}(z,\sigma(z))\) is of dimension 2 then \(\mathrm{acl}(z,\sigma(z)) = \mathrm{acl}(x,t) = \mathrm{acl}(y',u')\) which contradicts the fact that \(x\) and \(y'\), \(t\) and \(u'\) are independent. Therefore all Galois conjugates of \(z\) over \(x,t,y',u'\) are interalgebraic over \(s'\), and so \(\dim z'=1\).

Since all vertices of the new diagram have dimension 1 over \(s'\), and since \(s'\) is included in the parameters, the diagram is indeed a group configuration.

We can apply the same trick to the new configuration to get a configuration where \(y \in \mathrm{dcl}(x,a)\).

Part 3. Change the configuration to an interalgebraic one such that \(\alpha_s, \beta_t\) are (generically) invertible functions.

Similarly to the previous part, we pick an independent realisation of the type of \(u\), \(u'\), extend the set of parameters to include \(u'\), and consider the canonical base \(x'\) of the \(\mathrm{tp}(x/s,t',y,z')\). By an argument similar to the argument of Part~2 we conclude that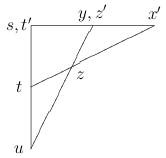

is a group configuration where \(x' \in \mathrm{dcl}(t,t',z,z')\), \(x' \in \mathrm{dcl}(s,y)\). Moreover, \(y \in \mathrm{dcl}(s,x)\), hence \(y \in \mathrm{dcl}(s,x')\). We need to show that \(z' \in \mathrm{dcl}(s,x')\). This follows from the fact that \(z' \in \mathrm{dcl}(s,x)\) becaus \(z\) has the same type as \(z'\) over \(s,x\).

Therefore in this new configuration \(\alpha_{s,t'}\) is generically an invertible function. A similar operation allows to pass to a configuration where \(\beta\) is invertible.

Variants of group configuration include statements where \(s,t,u\) are not of rank 1 (as for example in the exposition of Bouscaren), where one doesn’t assume finite rank at all: see Pillay’s book for the the stable context, and the article of Kim, de Pioro and Millar for simple theories with 4-amalgamation. A note in passing: the chain of modifications of the group configuration involves arbitrary extension of the base set of parameters, which is not canonical, 4-amalgamation allows to descend back to the base set of parameters (though, again, in an a priori non-canonical way). A variation of a group configuration-type statement is used in the book of Zilber’s, though the parts 2 and 3 of the proof above are absent there, due to a specific context that allows to guarantee that \(\alpha\) and \(\beta\) are generically functions.

Terry Tao presents an account of group configuration in the setting of qualitative probability theory.

A higher-dimensional group configuration sometimes allows to conclude the existence of supplementary algebraic structure. Due to hard result of Cherlin, a two-dimensional group acting on a one-dimensional set must be the affine group (that is, the semi-direct product of \(\mathbb{G}_m\) and \(\mathbb{G}_a\)) acting on the affine line, and a three-dimensional group acting on a one-dimnsional set is \(\mathrm{PGL}_2(K)\) for some definable field. The machinery of indiscernible arrays (presented in Hrushovski’s PhD thesis, and quoted in the paper of Hrushovski and Zilber, for examplex) allows to establish the existence of the field directly.

References